As part of the work leading to his Noble Prize, William Sharpe noted that in equilibrium all investors should hold some combination of the risk-free asset and the market portfolio. More risk averse investors would hold a larger proportion of the risk-free asset, while those willing to take greater risk could choose to leverage their holding of the market portfolio. From this fact, Sharpe derived what came to be called the Sharpe ratio relating risk and return. The ratio is given by:
(Expected Return – Risk-free rate) / Standard Deviation of Returns
In practice, the Sharpe ratio is estimated as follows. For a specified period, the average return on a portfolio is calculated and the average risk-free rate (usually given by the rate on short-term Treasury bills) is deducted. The difference is then divided by the standard deviation of the returns of the portfolio. For example, over the four-year period from 2020 to 2023 the average return on the S&P 500 was 11.81%, the average 90-day Treasury bill rate was 1.74%, and the standard deviation of the returns on the market portfolio was 23.01%. Applying equation (1), those inputs produce a Sharpe ratio of 0.44. In theory, no other portfolio should produce a higher Sharpe ratio, but in practice this is clearly counterfactual. For instance, a portfolio composed of the magnificent 7 stocks had a much higher Sharpe ratio over the four-year period. The reason is that the theory is based on expected returns, while practice uses actual returns. Because expected returns and actual returns can diverge widely over any particular time period, the Sharpe ratio is a noisy estimate of the relation between risk and return.
There is another interesting feature of the Sharpe ratio that has led to controversy over the years – the use of the standard deviation of returns to measure risk. Sharpe arrived at that measure by making a series of restrictive assumptions that do not hold in practice, but he hoped would be reasonable approximations. Though alternative risk measures have been proposed, no alternative has gained widespread adoption in practice, and the Sharpe ratio remains the lynchpin for assessing investment performance.
A simple alternative measure of risk is the frequency of large daily losses of 1%, 2% or 3%. It is after such market drops that the financial media focuses on stock market risk. There is much hand wringing about what caused the sell off and what it portends for the future. For this reason, we thought it would be interesting to assess the frequency of such drops and to compare the results with the standard deviation of returns. The findings are reported in the chart below for drops of 3% of more. Each column of the charts plots the number of daily drops of the stated magnitude each year from January 1, 1963 through May 23, 2024 (2024 is a partial year).
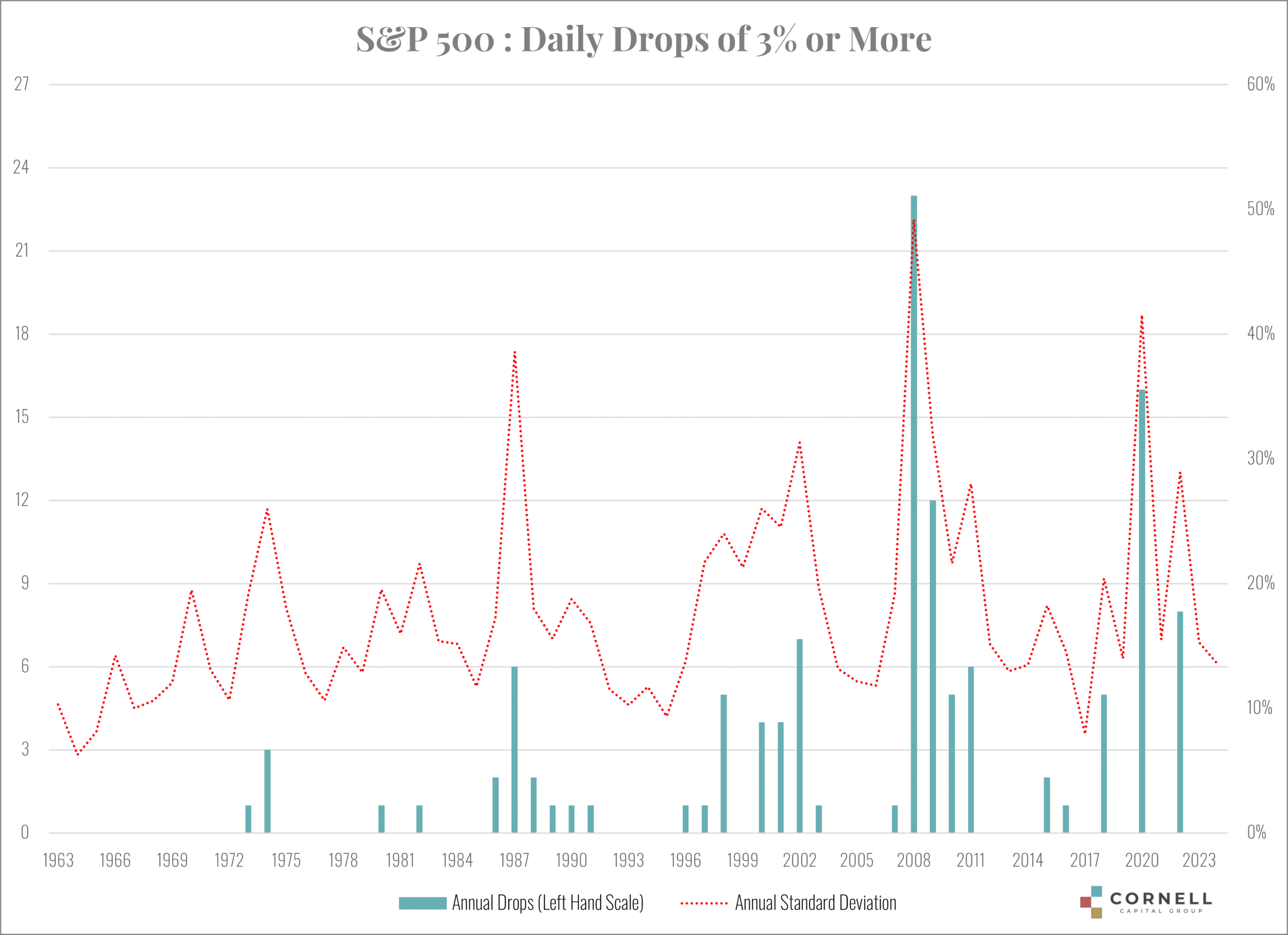
The most interesting way to read the charts is to start at the end, the 3% drop, and work back. Drops of 3% are dramatic. At the current level of the S&P 500, a 3% drop translates into a decline of more than 150 points in the index. As the chart shows, such drops are rare and tend to come in bunches. What is perhaps most surprising is that over more than a decade from January 1, 1963 through November 19, 1973 there was not one drop of more than 3% in the S&P 500! That decade of quiescence ends with the bear market of 1973 to 1974 during which the S&P fell almost 50%. Even so there were only four drops of 3% or more during the bear market. More recently, five periods stand out as producing 3% drops. They are the period surrounding the one-day 20.5% market crash in 1987, the collapse of the dot.com bubble, the great financial crisis which accounted for the most 3% drops, the Covid collapse, and the selloff in 2022 following the post Covid run-up. Interestingly, the last 3% drop was on September 13, 2022 and the last 2% drop was on December 15, 2022. Since then, the market has been relatively quiet, and the standard deviation has fallen back to a level associated with only background noise.
The charts for 1% and 2% drops tell basically the same story. The six crisis periods stand out, although not as clearly as for the 3% chart because the drops are more numerous.
Events like the six crises are often referred to as examples of market up and down “cycles.” But that is loose language. If they were cyclical, in the sense that the seasons are cyclical, smart investors would opportunistically sell in anticipation of the cyclical decline and thereby cause it to occur immediately. Instead, the crises are, as they must be in a competitive market, unpredictable occurrences. No one knows when the next will occur but given history it is reasonable to assume that one will. What the charts highlight is that the primary risk to equity investing is not the day-to-day gyrations in prices, but the large unpredictable drawdowns associated with the crises.
The charts also include a plot of the standard deviation for each year shown as a dotted red line. The standard deviation can be thought of as reflecting two components. First, background noise with the daily gyrations in prices. Second, the major price movements associated with crises. The second component is related to the large drops which by mathematical necessity cause the standard deviation to spike. As a result, the frequency of the large drops and the level of the estimated standard deviation are highly correlated. Nonetheless, the two measures are not identical, and we believe looking at both gives a deeper appreciation of the nature of the risk of equity investing.
There is one last point to note in closing. All six of the periods during which major drops were concentrated followed a point in time in which stocks were expensive relative to fundamentals such as earnings and cash flow. Currently, stocks are extremely expensive relative to earnings and cash flow. It gives one pause.
